A. Penjumlahan Bilangan dalam BCD
BCD merupakan penetapan langsung dari setara binernya. Kode tersebut juga
dikenal sebagaikode BCD 8421 yang menunjukkan bobot untuk masing-masing
kedudukan bitnya.
Sebagai contoh, bilangan desimal 1996 dapat dikodekan menurut BCD sebagai:
1996 = 0001 1001 1001 0110
1 9 9 6
Perlu diperhatikan bahwa pengubahan suatu bilangan desimal ke bilangan biner
berbeda dengan pengkodean suatu bilangan desimal meskipun hasilnya sama-sama
berupa suatu deretan bit. Untuk kode BCD ini, kode bilangan desimal 0 sampai dengan 9
sama dengan bilangan biner setaranya.
Namun untuk bilangan di atas 9, kode BCD berbeda dengan bilangan biner
setaranya. Misalnya biner untuk angka 11 adalah 1011, Letapi kode BCD untuk 11 adalah
0001 0001. Oleh karena itu, perlu diingat bahwa suatu deretan bit (angka) 0 dan 1 dalam
suatu sistem digital kadang-kadang mewakili suatu bilangan biner dan pada saat yang lain
merupakan informasi diskrit yang ditentukan oleh suatu kode biner tertentu. Keunggulan
utama kode BCD adalah mudahnya mengubah ke bilangan desimal. Kerugiannya adalah
sandi tidak akan berlaku untuk operasi matematika yang hasilnya melebihi 9.
Kode BCD hanya menggunakan 10 dari 16 kombinasi yang tersedia. Enam
kelompok bit yangtidak terpakai adalah 1010, 1011, 1100, 1101, 1110, dan 1111. Kode
BCD merupakan kode radiks campuran, dalam setiap kelompok 4 bitnya merupakan
sistem biner, tetapi merupakan decimal untuk kelompok demi kelompoknya.
Bentuk biner jika dinyatakan dalam bilangan desimal memerlukan 4 bit data.
Kombinasi 4 bitdata jika dimanfaatkan seluruhnya akan didapatkan kemungkinan 16
informasi yang berbeda. Dan 16 informasi ini untuk kode BCD hanya digunakan 10
informasi, sedangkan 6 informasi yang lain tidak diperlukan. Tabel 3.13 memperlihatkan
bilangan biner, desimal dan heksadesimal dibandingkan terhadap bentuk kode BCD.
Tabel 3.13 Kode BCD

Keterangan:
1) Echte Tetraden (8421 Kode)
2) Pseudotetrades
*) Dinyatakan pada tempat kedua (dikoreksi sebagai puluhan dan satuan)
Jika kita bandingkan bentuk bilangan di atas dengan bentuk BCD, tampak bahwa
setiap tempat dari bilangan desimal memerlukan 4 grup (tetrade) dan bilangan biner dan
tetrade ini tidak lagi dinyatakan dalam bilangan heksadesimal tetapi dalam bilangan
desimal. Kombinasi yang termasukdalam BCD Kode dinyatakan sebagai Echte Tetraden
sedangkan informasi yang tidak termasuk dalam BCD Kode dinyatakan sebagai
Pseudotetrades. Keheradaan Pseudotetrades dalam operasi aritmetika mempunyai arti
yang sangat penting, yaitu bahwa hasil operasi aritmetika tidak diizinkan berada di daerah
Pseudotetrades. Jika hasil operasi aritmetika dalam BCD Kode berada pada daerah
Pseudotetrades maka hasil operasi tersebut harus dikoreksi.
Penjumlahan bilangan dalam kode BCD dikerjakan seperti halnya penjumlahan
bilangan biner. jika hasil penjumlahan berada pada daerah Pseudotetrade, maka harus
dilakukan koreksi dengan cara menambahkan hasil dengan 610 = 01102.
Contoh :
Bilangan A = 0011 dan B = 0110 dalam bentuk BCD akan ditambahkan,
Bilangan A = 00112
BilanganB = 01102
---------- +
Hasil Sementara = 10012
Koresksi = tidak diperlukan karena hasilnya berada di Pseudotetrades
Hasil = 10012 (bentuk BCD)
Contoh :
Bilangan A = 0111 dan B = 1000 dalam bentuk BCD akan ditambahkan,
Bilangan A = 01112
Bilangan B = 10002
---------- +
Hasil Sementara = 11112
Koreksi = 01102 diperlukan karena berada di Pseudotetrades
Hasil =101012
Jadi: penjumlahan di atas menghasilkan 0001 ( puluhan) 0101 (satuan) (bentuk BCD)
Koreksi pada contoh 2 menghasilkan simpanan untuk tempat yang lebih tinggi
(puluhan),sehingga hasil penjumlahan setelah dikoreksi menghasilkan bilangan desimal 2
tempat yaitu 1(satu) puluhan dan 5 (lima) satuan yang dalam bilangan desimal disebut 15
(lima belas) sebagaihasil penjumlahan antara 710 (tujuh) dengan 810 (delapan). Untuk
penjumlahan bilangan yang lebih besar dapat dilakukan seperti pada contoh di atas.
Hanya saja harus diperhatikan cara-cara mengoreksi setiap hasil sementaranya.
Contoh
Bilangan A dan B dalam bentuk BCD akan ditambahkan,
Bilangan A = 01112 00112 10002
Bilangan B = 01012 01002 10012
Simpanan = 111 1111
Hasil Sementara = 11002 10002 1 00012
Koreksi = 01102 00002 01102
Simpanan = 1
Hasil = 12 00102 10002 01112
110 210 810 710
Dari contoh di atas, koreksi tidak hanya terjadi pada hasil yang berada di daerah
Pseudotetrades saja. Akan tetapi juga terjadi pada tetrade yang menghasilkan simpanan
walaupun tetrade tersebut tidak berada pada daerah Pseudotetrades.
B. Pengurangan Bilangan dalam BCD
Pengurangan bilangan dalam kode BCD dikerjakan seperti pengurangan pada
bilangan biner,yaitu dilakukan melalui langkah terbalik penjumlahan komplemen.
Komplemen satu dan komplemendua pada pengurangan bilangan dalam kode BCD ini
dinyatakan dalam komplemen sembilan dankompleman sepuluh. Komplemen sembilan
dibentuk melalui perbedaan nilai terhadap nilai tertinggidan bilangan desimal yaitu 910.
Sedangkan komplemen sepuluh dibentuk melalui increment dankomplemen sembilan
sehingga dapat dituliskan,
Komplemen sepuluh = Komplemen Sembilan + 1
K (10 ) = K ( 9 ) + 1
Contoh
Komplemen sembilan dan bilangan A = 0110 dalam bentuk BCD adalah,
Bilangan BCD tertinggi = 10012
Bilangan A = 01102
--------- -
K(9)dariA = 00112
Contoh
Komplemen sepuluh dan Bilangan B = 0111 dalam bentuk BCD adalah,
Bilangan BCD tertinggi = 10012
Bilangan B = 01102
K(9) dari B = 00102
K(10)dariB = 00112
Bentuk komplemen untuk bilangan yang besar (mempunyai beberapa tempat) dalam
kode BCD dapat dilihat pada contoh di bawah ini.
Contoh
Dari bilangan A = 0111 0100 100 = 74810 dalam bentuk BCD akan dibentuk komplemen
Sembilan dan komplemen sepuluh,
Bilangan BCD tertinggi = 10012 10012 10012
Bilangan A = 01102 01002 10002
K(9) dari A = 00102 01012 00012
K(10)dariA = 00112 01012 00102
Contoh di atas menunjukkan bahwa pembentukan K(10) dilakukan dengan cara
pembentukanK(9) pada setiap tempat terlebih dahulu dan terakhir baru di-increment untuk
mendapatkan K(10).
Proses pengurangan dapat dilakukan melalui penambahan dengan komplemen
sepuluh yangkemudian hasilnya masih perlu dikoreksi. Jika setelah dikoreksi masih
terdapat simpanan, makasimpanan tersebut tidak menunjukkan nilai bilangan tetapi hanya
menunjukkan tanda bilangan. Simpanan 1 menunjukkan tanda + (plus) sedangkan
simpanan 0 (tanpa simpanan) menunjukkan tanda - (minus). Jika terdapat tanda - (minus),
maka hasilnya masih harus dilakukan komplemen sepuluh sekali lagi.
BAB IV
Arithmatic Logic Unit (ALU)
Arithmatic Logical Unit (ALU), adalah salah satu bagian/komponen dalam sistem di dalam sistem komputer yang berfungsi melakukan operasi/perhitungan aritmatika dan logika (Contoh operasi aritmatika adalah operasi penjumlahan dan pengurangan, sedangkan contoh operasi logika adalah logika AND dan OR. ALU bekerja besama-sama memori, di mana hasil dari perhitungan di dalam ALU di simpan ke dalam memori.
Ada 3 jenis adder:
1) Rangkaian Adder dengan menjumlahkan dua bit disebut Half Adder.
2) Rangkaian Adder dengan menjumlahkan tiga bit disebut Full Adder.
3) Rangkain Adder dengan menjumlahkan banyak bit disebut Paralel Adder
- 1. HALF ADDER
Rangkaian Half Adder merupakan dasar penjumlahan bilangan Biner yang terdiri dari satu bit, oleh karena itu dinamai Penjumlah Tak Lengkap.
- jika A = 0 dan B = 0 dijumlahkan, hasilnya S ( Sum ) = 0.
- jika A = 0 dan B = 1 dijumlahkan, hasilnya S ( Sum ) = 1.
- jika A = 1 dan B = 1 dijumlahkan, hasilnya S ( Sum ) = 0
- jika A = 1 dan B =1 dijumlahkan, hasilnya S ( Sum ) = 0. dengan nilai pindahan cy(Carry Out) = 1
Dengan demikian, half adder memiliki 2 masukan ( A dan B ) dan dua keluaran (S dan Cy).
- 2. FULL ADDER
Pada saat sekarang ini sebuah chip/IC dapat mempunyai beberapa ALU sekaligus yang memungkinkan untuk melakukan kalkulasi secara paralel. Salah satu chip ALU yang sederhana (terdiri dari 1 buah ALU) adalah IC 74LS382/HC382ALU (TTL). IC ini terdiri dari 20 kaki dan beroperasi dengan 4×2 pin data input (pinA dan pinB) dengan 4 pin keluaran (pinF).
Arithmatic Logical Unit (ALU), fungsi unit ini adalah untuk melakukan suatu proses data yang berbentuk angka dan logika, seperti data matematika dan statistika. ALU terdiri dari register-register untuk menyimpan informasi.Tugas utama dari ALU adalah melakukan perhitungan aritmatika (matematika) yang terjadi sesuai dengan instruksi program. Rangkaian pada ALU (Arithmetic and Logic Unit) yang digunakan untuk menjumlahkan bilangan dinamakan deACE=”Verdana, sans-serif”>Sebuah Full Adder menjumlahkan dua bilangan yang telah dikonversikan menjadi bilangan-bilangan biner. Masing-masing bit pada posisi yang sama saling dijumlahkan. Full Adder sebagai penjumlah pada bit-bit selain yang terendah. Full Adder menjumlahkan dua bit input ditambah dengan nilai Carry-Out dari penjumlahan bit sebelumnya. Output dari Full Adder adalah hasil penjumlahan (Sum) dan bit kelebihannya (carry-out).
- 3. PARALEL ADDER
Rangkaian Parallel Adder adalah rangkaian penjumlah dari dua bilangan yang telah dikonversikan ke dalam bentuk biner. Anggap ada dua buah register A dan B, masing-masing register terdiri dari 4 bit biner : A3A2A1A0 dan B3B2B1B0.
Rangkaian Parallel Adder terdiri dari Sebuah Half Adder (HA) pada Least Significant Bit (LSB) dari masing-masing input dan beberapa Full Adder pada bit-bit berikutnya. Prinsip kerja dari Parallel Adder adalah sebagai berikut : penjumlahan dilakukan mulai dari LSB-nya. Jika hasil penjumlahan adalah bilangan desimal “2” atau lebih, maka bit kelebihannya disimpan pada Cout, sedangkan bit di bawahnya akan dikeluarkan pada Σ. Begitu seterusnya menuju ke Most Significant Bit (MSB)nya.
Tugas lain dari ALU adalah melakukan keputusan dari operasi sesuai dengan instruksi program yaitu operasi logika (logical operation). Operasi logika meliputi perbandingan dua buah elemen logika dengan menggunakan operator logika.
- Arithmatic Logical Unit (ALU):
Bertugas membentuk fungsi – fungsi pengolahan data komputer. ALU sering disebut mesin bahasa (machine language) karena bagian ini mengerjakan instruksi – instruksi bahasa mesin yang diberikan%”> .
Pada saat sekarang ini sebuah chip/IC dapat mempunyai beberapa ALU sekaligus yang memungkinkan untuk melakukan kalkulasi secara paralel. Salah satu chip ALU yang sederhana (terdiri dari 1 buah ALU) adalah IC 74LS382/HC382ALU (TTL). IC ini terdiri dari 20 kaki dan beroperasi dengan 4×2 pin data input (pinA dan pinB) dengan 4 pin keluaran (pinF).
Arithmatic Logical Unit (ALU), fungsi unit ini adalah untuk melakukan suatu proses data yang berbentuk angka dan logika, seperti data matematika dan statistika. ALU terdiri dari register-register untuk menyimpan informasi.Tugas utama dari ALU adalah melakukan perhitungan aritmatika (matematika) yang terjadi sesuai dengan instruksi program. Rangkaian pada ALU (Arithmetic and Logic Unit) yang digunakan untuk menjumlahkan bilangan dinamakan de padanya.
ALU terdiri dari dua bagian, yaitu unit arithmetika dan unit logika boolean, yang masing – masing memiliki spesifikasi dan tugas tersendiri. Fungsi-fungsi yang didefinisikan pada ALU adalah Add (penjumlahan), Addu (penjumlahan tidak bertanda), Sub (pengurangan), Subu(pengurangan tidak bertanda), and, or,xor, sll (shift left logical), srl (shift right logical), sra (shift right arithmetic), dan lain-lain.
Arithmetic Logical Unit (ALU) merupakan unit penalaran secara logic. ALU ini merupakan Sirkuit CPU berkecepatan tinggi yang bertugas menghitung dan membandingkan. Angka-angka dikirim dari memori ke ALU untuk dikalkulasi dan kemudian dikirim kembali ke memori. Jika CPU diasumsikan sebagai otaknya komputer, maka ada suatu alat lain di dalam CPU tersebut yang kenal dengan nama Arithmetic Logical Unit (ALU), ALU inilah yang berfikir untuk menjalankan perintah yang diberikan kepada CPU tersebut.
ALU sendiri merupakan suatu kesatuan alat yang terdiri dari berbagai komponen perangkat elektronika termasuk di dalamnya sekelompok transistor, yang dikenal dengan nama logic gate, dimana logic gate ini berfungsi untuk melaksanakan perintah dasar matematika dan operasi logika. Kumpulan susunan dari logic gate inilah yang dapat melakukan perintah perhitungan matematika yang lebih komplit seperti perintah “add” untuk menambahkan bilangan, atau “devide” atau pembagian dari suatu bilangan. Selain perintah matematika yang lebih komplit, kumpulan dari logic gate ini juga mampu untuk melaksanakan perintah yang berhubungan dengan logika, seperti hasil perbandingan dua buah bilangan.
Instruksi yang dapat dilaksanakan oleh ALU disebut dengan instruction set. Perintah yang ada pada masing-masing CPU belum tentu sama, terutama CPU yang dibuat oleh pembuat yang berbeda, katakanlah misalnya perintah yang dilaksanakan oleh CPU buatan Intel belum tentu sama dengan CPU yang dibuat oleh Sun atau perusahaan pembuat mikroprosesor lainnya. Jika perintah yang dijalankan oleh suatu CPU dengan CPU lainnya adalah sama, maka pada level inilah suatu sistem dikatakan compatible. Sehingga sebuah program atau perangkat lunak atau software yang dibuat berdasarkan perintah yang ada pada Intel tidak akan bisa dijalankan untuk semua jenis prosesor,kecuali untuk prosesor yang compatible dengannya.
Transistor Transistor logic (TTL) adalah desain logika digital di mana transistor bipolar bertindak atas pulsa arus langsung. Banyak gerbang logika TTL dibuat ke dalam satu sirkuit terpadu (IC). TTL IC memiliki empat digit dimulai dengan 74 (74LS02, 74S00).
TTL menggunakan transistor dengan beberapa emiten di gerbang yang memiliki lebih dari satu input. TTL ditandai oleh kecepatan switching yang tinggi (dalam beberapa kasus diatas 125 MHz), dan kekebalan relatif terhadap noise.
Kelemahan Sirkuit - menarik arus lebih dari sirkuit yang setara menggunakan logika semikonduktor oksida logam (MOS). TTL arus rendah, tetapi permintaan berkurang dengan mengorbankan kecepatan operasi.
Tingkat Logika
TTL tergantung pada 5V Logic Levels. Sirkuit dibangun dari transistor bipolar untuk mencapai switching dan mempertahankan status logika. Transistor pada dasarnya untuk switch yang dikontrol secara elektrik.
Input & Output Voltage Levels
➽ Tegangan output minimum TINGGI (VOH) adalah 2,7 V.
Tegangan output dari perangkat bergerak ke TINGGI setidaknya 2,7 V.
➽ Tegangan input TINGGI minimum (VIH) adalah 2 V.
Setiap tegangan minimal 2 V akan dibaca sebagai logika 1 (TINGGI)
➽ Bantalan 0,7 V antara output dari satu perangkat
dan masukan dari perangkat lain. Disebut sebagai Noise Margin.
➽ Tegangan output LOW maksimum (VOL) adalah 0,4 V.
Berarti perangkat mencoba mengirim logika 0 akan selalu di bawah 0,4 V.
➽ Tegangan input LOW maksimum (VIL) adalah 0,8 V.
Setiap sinyal input yang berada di bawah 0,8 V
Masih dianggap sebagai logika 0 (RENDAH).
Digital Logic Voltage Levels
Antara nilai TINGGI dan RENDAH, terdapat "Tanah tak bertuan" (area biru di bawah) dan jika menerapkan tegangan sinyal, tidak tahu apakah gerbang logika akan meresponnya sebagai level "0" atau sebagai level "1", dan hasilnya akan menjadi tidak dapat diprediksi.
Kebisingan adalah tegangan acak dan tidak diinginkan yang diinduksi ke dalam sirkuit elektronik oleh gangguan eksternal, seperti
➽ Switch terdekat
➽ Fluktuasi pasokan listrik
➽ Kabel dan konduktor
➽ Radiasi elektromagnetik lain yang nyasar.
Kemudian agar gerbang logika tidak dipengaruhi oleh kebisingan harus memiliki sejumlah batas kebisingan atau kekebalan kebisingan.
Transistor Transistor Logic
Keluarga logika menggunakan transistor dengan beberapa emiten. Secara komersial dimulai dengan seri 74 seperti 7404, 74S86 dll. Tahun 1961 oleh James L Bui dan secara komersial digunakan dalam desain logika tahun 1963.
1. Open Collector Output
Transistor Q1 sebagai kelompok dioda yang ditempatkan kembali ke belakang.
Dengan salah satu input pada logika rendah, junction basis emitor yang sesuai bias maju dan penurunan tegangan di dasar Q1 sekitar 0.9V, tidak cukup untuk transistor Q2 dan Q3 melakukan nya.
Jadi output mengambang atau Vcc, yaitu tingkat Tinggi. Ketika semua input tinggi, semua jeda emitor basis Q1 adalah reverse bias dan transistor Q2 dan Q3 mendapatkan arus basis yang cukup dan berada dalam mode saturasi.
Output pada logika rendah. (Transistor menuju saturasi, arus kolektor harus lebih besar dari β kali arus basis).
2. Totem Pole Output
Penambahan rangkaian Pull-Up aktif dalam output Gerbang, menghasilkan pengurangan Delay Propagasi. Operasi logika sama dengan output kolektor terbuka.
Penggunaan transistor Q4 dan diode adalah untuk menyediakan pengisian cepat dan pemakaian kapasitansi parasit di Q3. Resistor digunakan untuk menjaga arus keluaran ke nilai yang aman.
3. Three state Gate
➽ Keadaan tingkat RENDAH,
Ketika transistor lebih rendah ON dan transistor atas OFF.
➽ Keadaan tingkat TINGGI,
Ketika transistor lebih rendah OFF, dan transistor atas ON.
➽ Status ketiga,
Ketika kedua transistor MATI.
Memungkinkan koneksi kawat langsung dari banyak output.
Keluarga
Transistor Transistor Logic
Antara nilai TINGGI dan RENDAH terletak pada bentuk TTL adalah Transistor Transistor Logic. Keluarga logika yang terbangun
➽ Transistor NPN
➽ Dioda sambungan PN
➽ Resistor
Blok dasar logika (Gerbang NAND) dan terbagi :
Transistor Transistor Logic - Standar
Transistor Transistor Logic - Daya Rendah
Transistor Transistor Logic - Daya Tinggi
Transistor Transistor Logic - Schottky
Desain untuk mempercepat waktu operasi. Kecepatan yang ditawarkan oleh jenis TTL ini, dua kali kecepatan yang ditawarkan oleh TTL daya tinggi. Disipasi daya untuk kedua TTL sama dan tidak ada konsumsi daya tambahan.
Perbaikan dalam desain sirkuit untuk memperhitungkan penundaan propagasi, konsumsi, persyaratan fan-in dan fan-out dll, jenis teknologi transistor bipolar TTL ini membentuk dasar dari keluarga IC logika digital "74". Seperti
➽ "7400" Quad 2-input AND gate
➽ "7402" Quad 2-input OR.

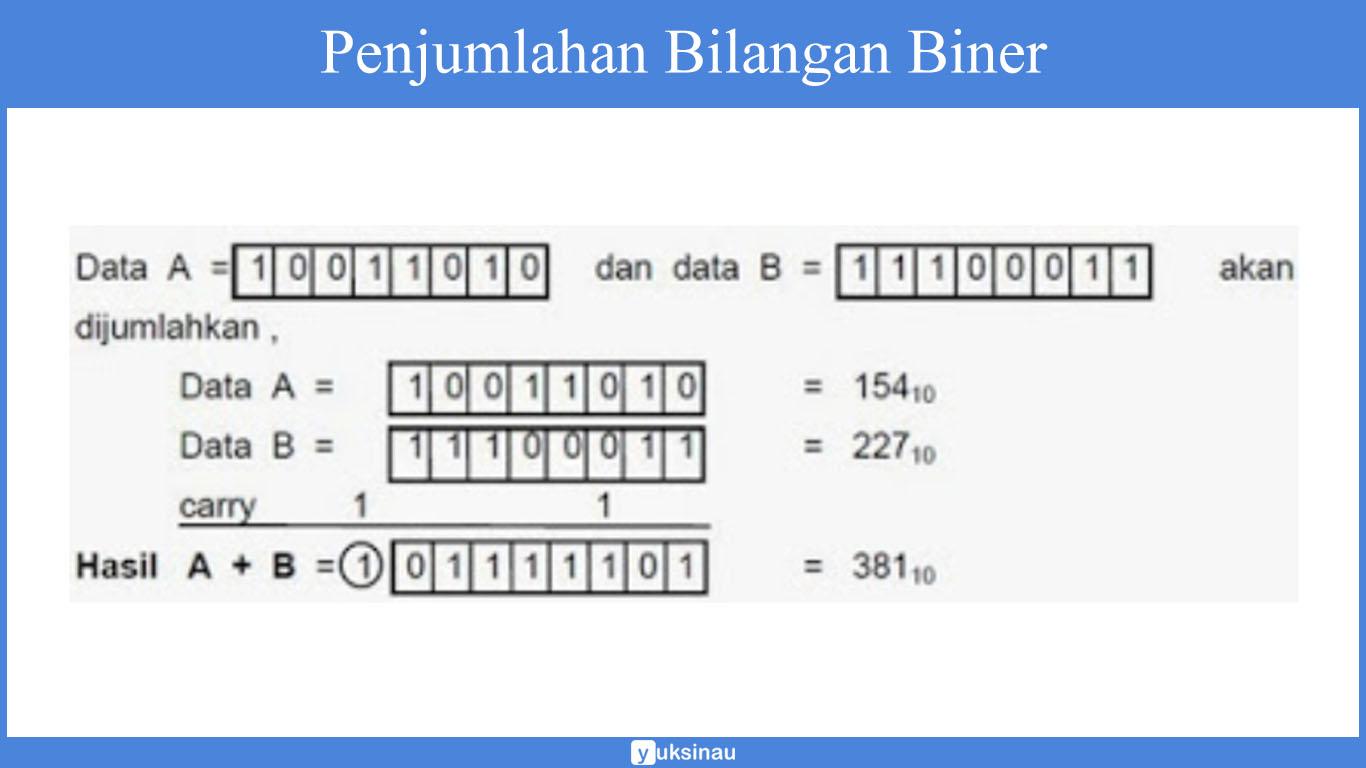

 Lalu
Lalu 


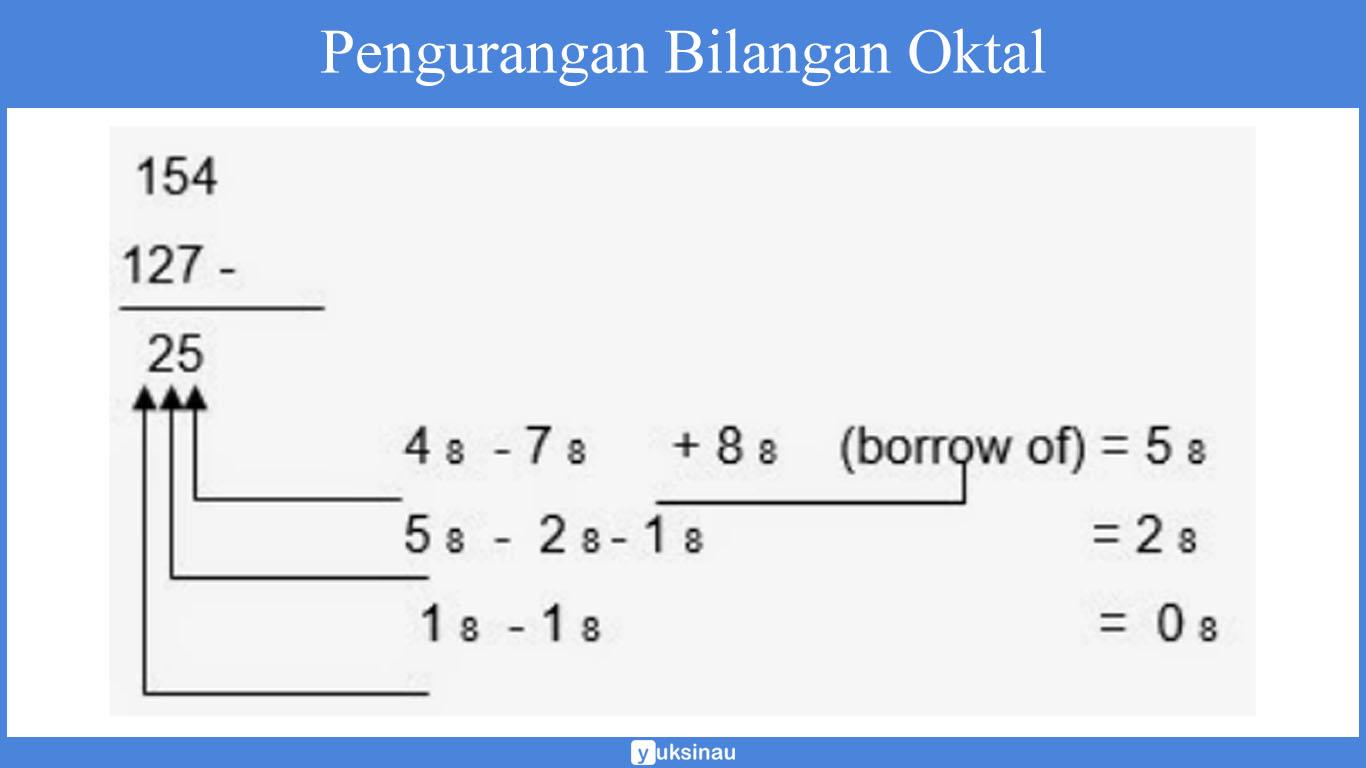

 3. Operasi Aritmatika Bilangan Heksadesimal
3. Operasi Aritmatika Bilangan Heksadesimal



















EmoticonEmoticon